Let's Understand How a CPU Works
Designing a CPU from the ground up, with no knowledge needed
Chapter 08 - Ripple Carry Adders
Topics Covered: Ripple-Carry Adders, Adder-Subtractor
Now that we know how to do simple addition using half adders and full adders (which are used to do one-bit addition), I believe we are ready to learn about ripple-carry adders (for, you guessed it, multi-bit addition). Moreover, we will get to learn why the carry-in bit was so crucial that we needed to create a half adder on steriods (the full adder).
Ripple Carry Adder
2-Bit Example
Imagine now we are adding two numbers: \(3_{10}\) and \(1_{10}\). In binary format, these numbers would be represented as \(11_{2}\) and \(01_{2}\) respectively. Essentially, our expression here can be represented as \(11_{2}+01_{2}\). Let’s add these values using a table.
| Third Bit (Carry Over) | Second Bit | First Bit | |
|---|---|---|---|
| Carry Over from Previous Column | 1 | 1 | |
| Number 3 | 1 | 1 | |
| Number 1 | 0 | 1 | |
| Result | 1 | 0 | 0 |
In the last chapter, we learned about Full Adders. It turns out that we can actually chain multiple Full Adders to do multi-bit addition and accurately represent carry-over logic. When we chain multiple Full Adders together, we can create a Ripple Carry Adder. Let’s break this down a bit further using our multi-bit example above.
Before we begin to build out the Ripple Carry Adder, let’s analyze how Full Adders can be used to do multi-bit additon. Notice from the example above how we have two bits for each of the numbers, we can use a full adder to do the addition for each corresponding bit (or each column of the table). So, essentially, we can use a full adder to represent the addition happening in the First Bit column and use another full adder to represent the addition happening in the Second Bit column. Each corresponding bit (in other words, each bit in the same position) will be added together from both binary values. This is pretty similar to how we do regular addition: add the one’s place, the ten’s place, the hundred’s place, and so on. We can begin building out the above example in circuit form below:
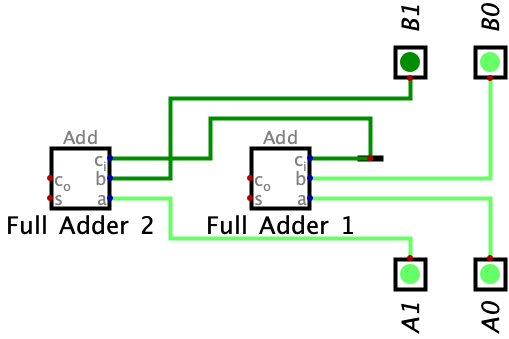
Aside: As you can see in the above, we don’t have our typical circuit with the gates. Usually when we build circuit diagrams, we try to simplify the circuit by using a schematic symbol. In this case, the box we have is used to represent a Full Adder instead of using the entire Full Adder circuit we built in Chapter 7 multiple times. However, you can see that this schematic symbol works in the same way as the circuit: we have 3 inputs (A, B, Carry-In) and 2 outputs (Sum and Carry-Out)
Aside: You might have also seen a weird looking symbol going into the carry-in input (the dash). This symbol is just supposed to represent a grounded input meaning it sends an electrical signal of 0 or off. Don’t worry about the carry-in input for the initial Full Adder of our Ripple Carry Adder circuit (we will get to this later).
Notice in the example above how each corresponding bit in the same place value goes to the same full adder (so the bits A1 and B1 go to Full Adder #1 and the bits A2 and B2 go to Full Adder #2). Intuitively, this makes sense because we are adding bits which are in the same place value (as mentioned earlier).
Now, let’s review how the carry-in bit comes into play. Notice how when we add the bits in the First Bit column, there’s a carry over? Well, we can use the carry-over bit outputted from the Full Adder 1 and insert it into the carry-in input in Full Adder 2. This is shown in the image below:
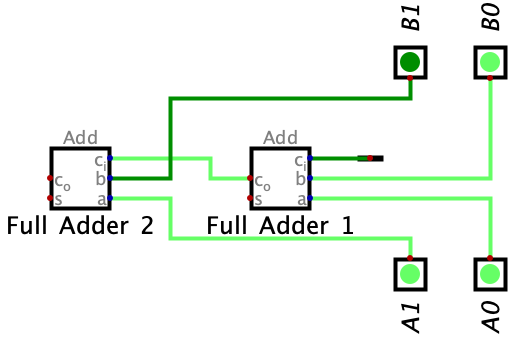
Notice how the wire going from the carry-out in Full Adder 1 to the carry-in in Full Adder 2 is light green (which means it carries the value of 1). This is important because we can use the carry-over bit to now do addition with multi-bit binary values. Without the carry-over output and the carry-in input on a full adder, we wouldn’t accurately be able to do multi-bit addition since the carry-over logic wouldn’t be supported. We are now on the way to building our first Ripple Carry Adder.
Let’s finish the circuit by displaying the output:
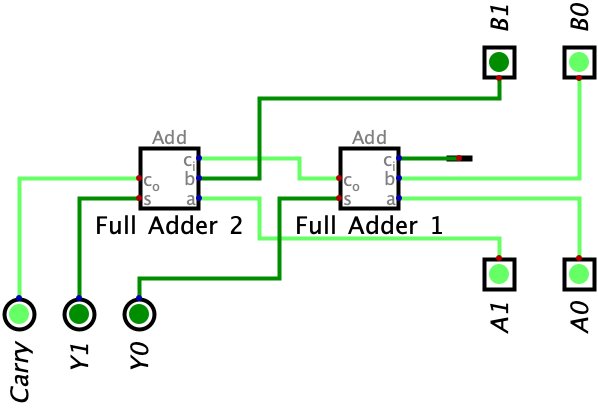
Congrats! You just built your first Ripple Carry Adder.
What the Carry Bit Means
In the example above, you might have noticed that the Carry output was on. Usually, Ripple Carry Adders are used to do unsigned binary addition (review Chapter 5 if you still are unclear on what this means). If you recall, in unsigned binary addition, we have an overflow when the Carry bit is on because we are adding 2 2-bit numbers, but our result needs 3-bits in order to be represented accurately. If this still doesn’t make sense, I’ll make it simple for you in a one-line: if the Carry bit is on after performing unsigned binary addition (which is what Ripple Carry adders do), we have an overflow. The example above is an example of overflow in unsigned addtion.
4-bit Example
Now, let’s try a slightly harder example. This time we will be added 2 4-bit binary values (the general rule for ripple carry adders is you can add 2 N-bit binary values at a time). So, just for example sake, I chose two random numbers: \(2_{10}\) and \(8_{10}\) (\(0010_{2}\) and \(1000_{2}\) in binary respectfully). We can create another table like we did for the last example:
| Fifth Bit (Carry Out) | Fourth Bit | Third Bit | Second Bit | First Bit | |
|---|---|---|---|---|---|
| Carry Over from Previous Column | 0 | 0 | 0 | 0 | |
| Number 2 | 0 | 0 | 1 | 0 | |
| Number 8 | 1 | 0 | 0 | 0 | |
| Result | 1 | 0 | 1 | 0 |
So the result of \(0010_{2}+1000_{2}\) was \(1010_{2}\) which is \(10_{10}\) (there is no overflow in this example either). Let’s build our ripple carry adder:
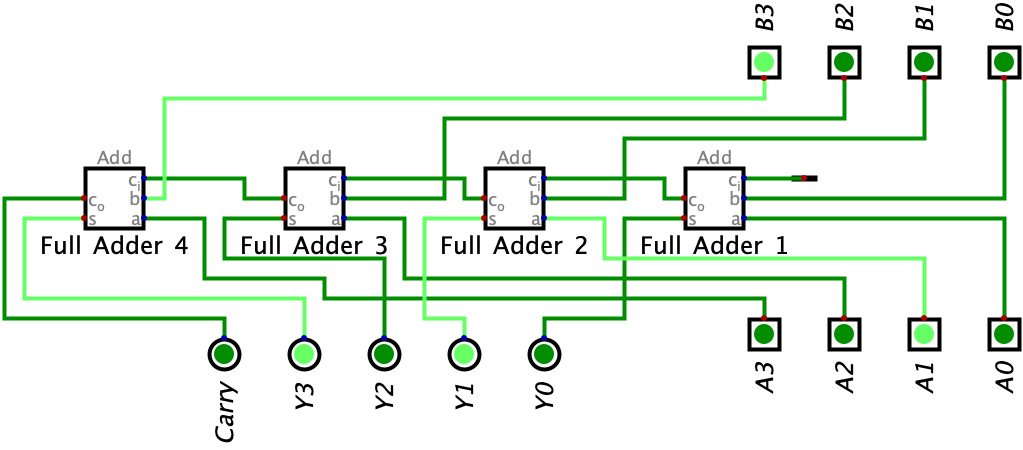
So again, we need to add the bits from the same place values and carry over the carry-over output of one full adder into the carry-in input of the next full adder when there is carry-over logic involved.
Adder-Subtractor
Now that you’re an expert in Full Adders and Ripple Carry Adders, it’s time for another round of roids. This time around we are going to create a circuit called the Adder-Subtractor. An Adder-Subtractor allows us to perform both binary addition and binary subtraction with the same circuit. We can tweak our Ripple Carry Adder to create the Adder-Subtractor. Before we introduce the circuit, let’s go over 2 important ideas that we need to know about first:
- When we want to find the value of a negative integer number in binary, we use two’s complement. Two’s complement follows three simple steps: find the binary representation of the positive version of the negative integer number, flip all the binary bits, and then add one to the result. Two’s complement can be crucial for doing binary subtraction. Instead of having to actually subtract binary values (\(B-A\)), we can find the two’s complement of the subtrahend and add the values instead (\(B+(-A)\)).
- We also need to learn what a 2-to-1 multiplexor is. Essentially, we have a selector bit (C in the truth table and circuit below) which chooses between two different inputs. So if we have two inputs, A and B, the A bit will be outputted if the selector bit is 0 and the B bit will outputted if the selector bit is 1. That’s it, simple right? Also, if you notice the below truth table looks a bit familar, it is! In Chapter 6, we actually went over how to build a switch circuit which is the same as the circuit shown below. Below, we are using a schematic to represent the circuit instead of building it again (this circuit will appear a few more times, so make sure you take the time to understand what it’s doing). Below I’ve included the truth table and an example of the circuit:
| C | A | B | Y |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
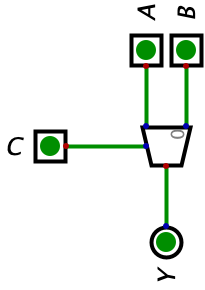
Cool, now that we reviewed binary subtraction and what multiplexors are, let’s review our goal for this section: we need to take the Ripple Carry Adder we learned about and the two ideas mentioned at the start of this section on Adder-Subtractors (binary subtraction and multiplexors) and modify the Ripple Carry Adder to also do subtraction. You might be thinking that is impossible, but let’s take a closer look at how we can modify our circuit to perform subtraction.
In our Adder-Subtractor circuit, we are responsible for doing addition which will work the same way as it does in a Ripple Carry Adder. However, to do subtraction (which can be represented by the expression \(B-A\)), we can use a trick that we learned in Chapter 5 and has already been mentioned a couple times in the past few paragraphs: two’s complement. This will allow us to work the expression \(B+(-A)\) (which is the equivalent of \(B-A\)) allowing us to sneakily be able to do addition for our subtraction problem. We want to convert our subtraction problem to addition for two reasons: it is easier to do addition than subtraction and since Ripple Carry Adders can only do addition, we already have a starting point. If we can figure out how to alter our expression (\(B-A\)) and implement the two’s complement conversion for Input A in our Ripple Carry Adder, we can essentially do subtraction with an adder circuit. Before I get into that, I hope you are starting to see how poweful two’s complement really is.
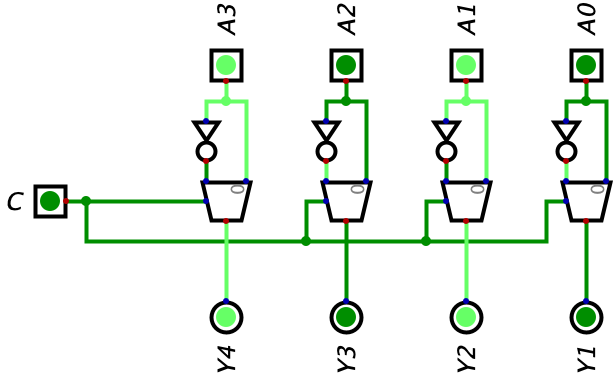
Essentially, when we do two’s complement, we are doing two main things (again, a review): flip all the bits of the subtrahend and add one. In order to flip all of the bits of the subtrahend, we did just learn about multiplexors, so let’s see what we can create with them. We know a multiplexor takes two inputs (A and B as shown in the truth table above). Instead of feeding the multiplexor two distinct inputs, we can also just feed use one input where the A input of the multiplexor is the value of the one input we have, but B input of the multiplexor is that value of the input we have, but inverted. Below, I provide an example of a multiplexor doing what I just explained:
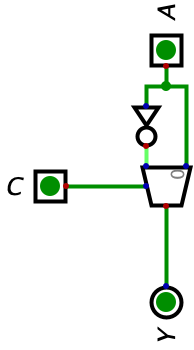
In the above example, \(A=0\) and \(C=0\). Since \(C=0\), the normal input will be selected and since \(A=0\), 0 is also outputted. However, when \(C=1\), the output changes because it will choose the inverted input as shown in the image below:
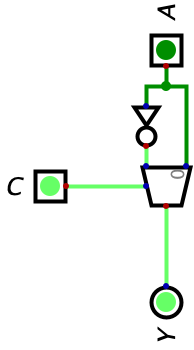
Notice how this pretty similar to flipping a bit. When \(C=0\), we are displaying the input un-changed, but when \(C=1\), we are displaying the inverted version of the bit. Let’s expand this idea to 4 bits in the image below:
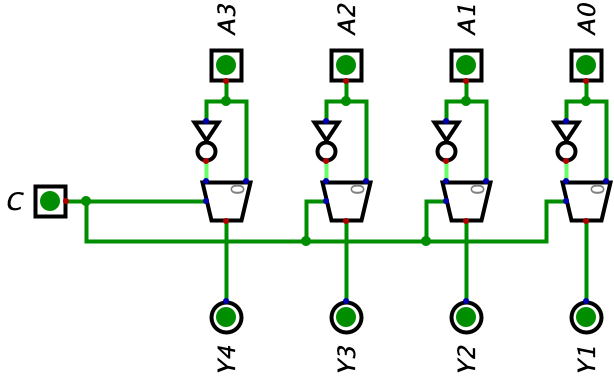
We can give the Input A a random value such as \(1010_{2}\) and test our theory that this circuit will be able either to keep the same version of the bits or flip the bits. When \(C=0\), here is our circuit outputting our normal, un-flipped binary value:
But, now the fun part. Let’s make \(C=1\) and check our circuit:
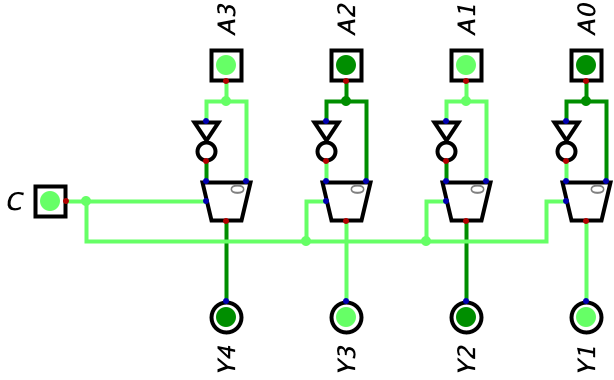
Woah! We were just able to flip all of our bits in our circuit by flipping the switch on the C input! With this circuit, we have achieved the first portion of performing two’s complement on a binary number: being able to flip all of the bits. I think a good next step would be trying to implement this into our Ripple Carry Adder circuit by altering Input A to flip its bits. This is because the expression we are trying to implement into our circuit is \(B-A\) and A is the subtrahend. I show in the circuit below:
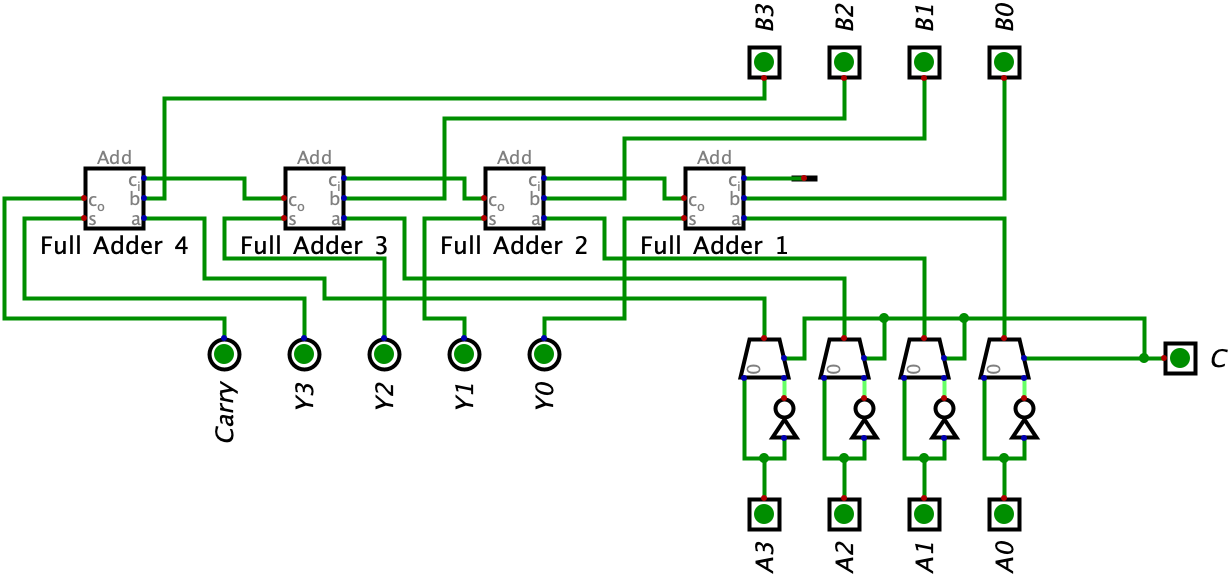
However, we are not yet done because we still have not completed the second step in finding the two’s complement on Input A: adding 1. In the image above, we can flip all the bits by turning on the C bit on. But, in order to find the two’s complement to Input A, we also need to add 1 to Input A. However, we cannot add 1 directly to Input A. Think about it for a second. In our circuit above, it would be kind of difficult to do that and it would also force us add further logic to our circuit which makes it more complicated.
Instead, what if we just added one to the whole equation in general? Let’s think about this for a quick second. Right now, we are attempting to perform subtraction with our Ripple Carry Adder by performing \(B+(-A)\) instead of \(B-A\) since it allows us to perform addition. However, what if we instead used the following equation to perform the subtraction: \(B+(~A)+1\). The ~ symbol represents the flipped bits and then the addition \(+1\) represents the second step of two’s complement. I surmise that the equation \(B+(~A)+1\) is the same as the equation \(B+(-A)\) because we are breaking down the two’s complement step we perform on Input A into two distinct steps in our equation. This means we can technically add the value of 1 anywhere in the circuit which makes it easier.
But you might be asking yourself where else in the circuit can the value of 1 be fed into. Notice how when we flip the bits for two’s complement, we need to turn on the C bit. Since this bit is already performing half the work for us by flipping everything, we can further use it to our advantage and feed the bit into the carry-in bit of Full Adder 1 which allows us to add an extra 1. So, when the C bit is on, we can also add 1 to the circuit alongside with flipping all the bits. But, let’s back up for a second. You might be wondering if we are breaking any rules or if it is even possible to use the carry-in bit of Full Adder 1. But remember, we created Full Adders for one reason and that is to use the carry-in bit. However, so far, the carry-in bit of Full Adder 1 has been totally unused. But now, we can use it to perform subtraction. I show an image of the circuit below where we feed the C input into the carry-in bit of Full Adder 1:
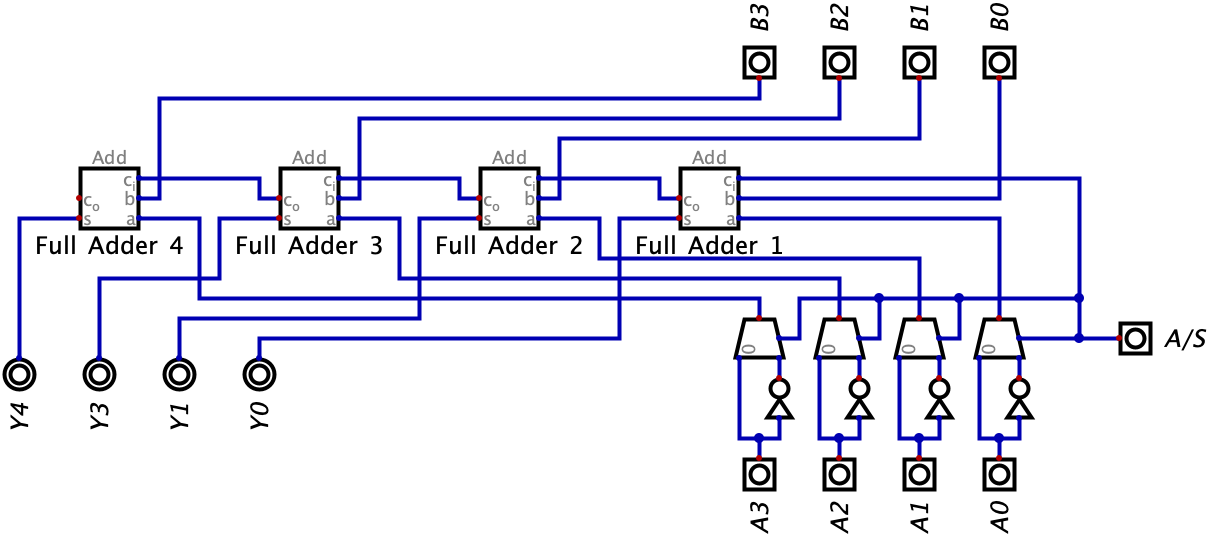
Cool right? You just created an Adder-Subtractor circuit. But before we start playing with examples, let’s go through a couple of important rules and points about how this circuit actually works:
- The first thing I would like discuss is our inputs. When using an adder-subtractor, we are going to normalize the inputs using two’s complement. So Input A (on the bottom) and Input B (on the top) should be using two’s complement form whether we are doing addition or subtraction. In our case, since we are only using 4 bits, we can only represent numbers from \(-8_{10}\) to \(7_{10}\).
- When the C bit is 0, it means we are doing addition. Again, this means we are choosing the normal input of A and nothing is being fed into the carry-in input of Full Adder 1. So essentially, when the C bit is turned off, we are just dealing with a Ripple Carry Adder.
- In the case of subtraction, we are able to use the two’s complement of the subtrahend when the C bit is 1 because it flips the bits of Input A and adds 1 to the entire circuit. This enables us to perform addition with Input B and the two’s complement version of Input A, represented by the equation \(B+(-A)\), instead of having to build a whole other circuit to do \(B-A\) (because remember we are dealing with adders and not subtractors).
- Lastly, as we read in Chapter 5, overflow can occur when dealing with binary values in two’s complement (again, overflow in two’s complement is equivalent to getting a positive result adding two negative values or a negative result adding two positive values meaning our result is out of range and cannot be represented accurately). So in order to build an overflow flag, we can use the equation \(A_{3} B_{3} \bar Y_{3} + \bar A_{3} \bar B_{3} Y_{3}\). The first side of this equation checks if input A and B are both negative (by checking if the MSBs have the value of 1) and the ouput is positive (by checking if the MSB is 0). The second side of the equation does the vice versa. It checks that the ouput is negative (by checking if the MSB has a value of 1), and input A and B are both positive (by checking the MSBs have the value of 0). The circuit below includes the overflow logic for our Adder-Subtractor circuit:
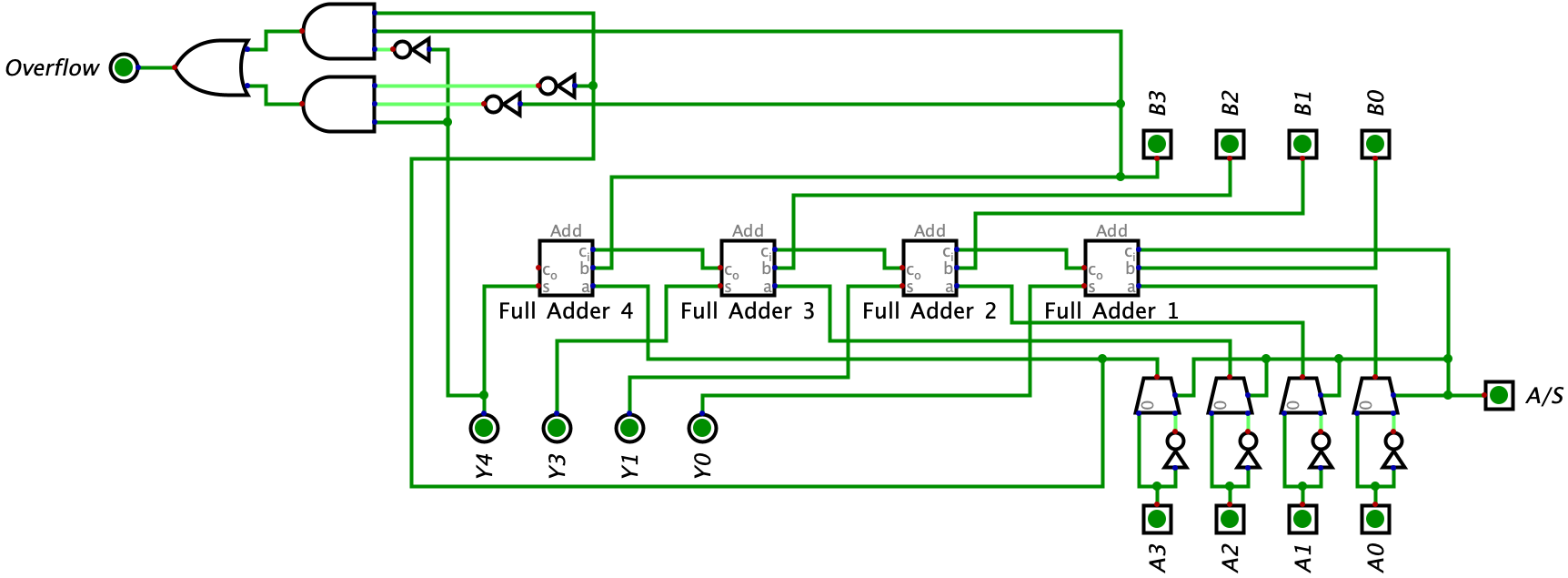
Now that we understand how the circuit functions at a deeper level, let’s take a look at a few examples. The first example I want to look at is basic addition. Again, addition in an adder-subtractor circuit works the same way it does in a ripple carry adder (but with two’s complement). Before we jump into the example, note that input A is \(0100_{2}\) and input B is \(0001_{2}\) (\(4_{10}\) and \(1_{10}\) respectively). Together, they should add to \(0101_{2}\) (\(5_{10}\)).
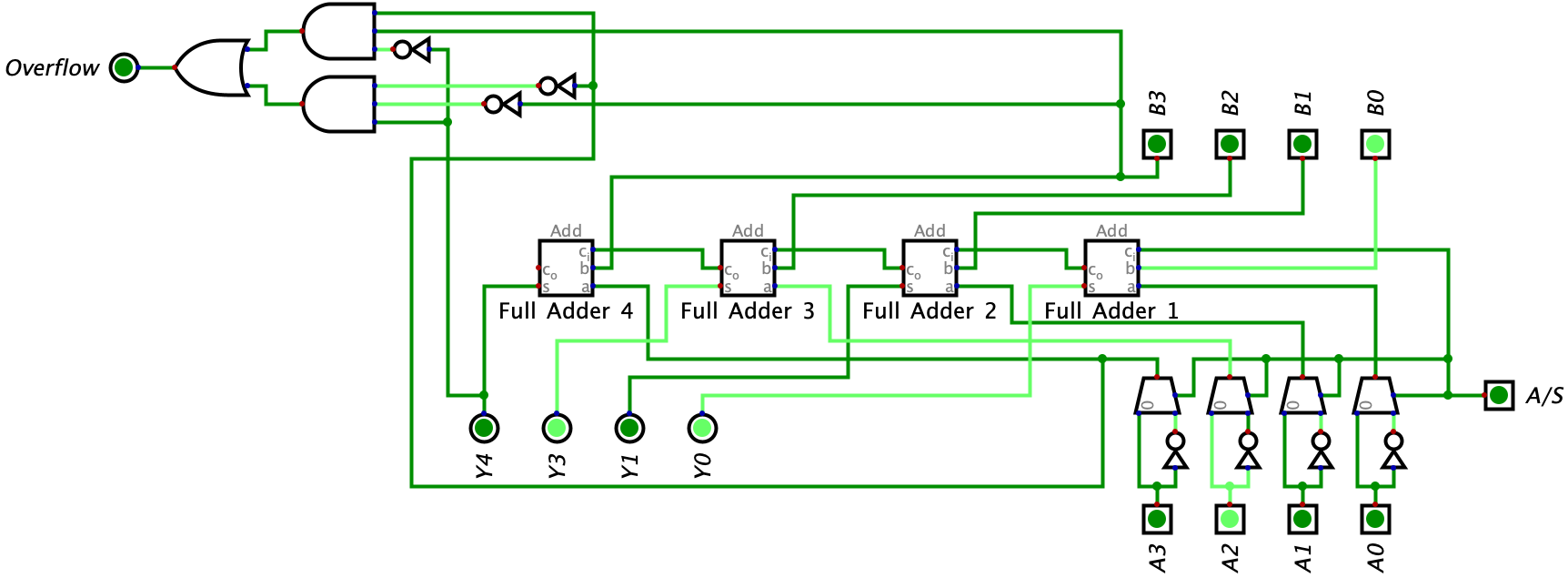
Now, we are going to take an example of addition which results in overflow. In this new example, input A is \(0100_{2}\) and input B is \(0100_{2}\) resulting in an overflow (I will let you work the math and logic out).
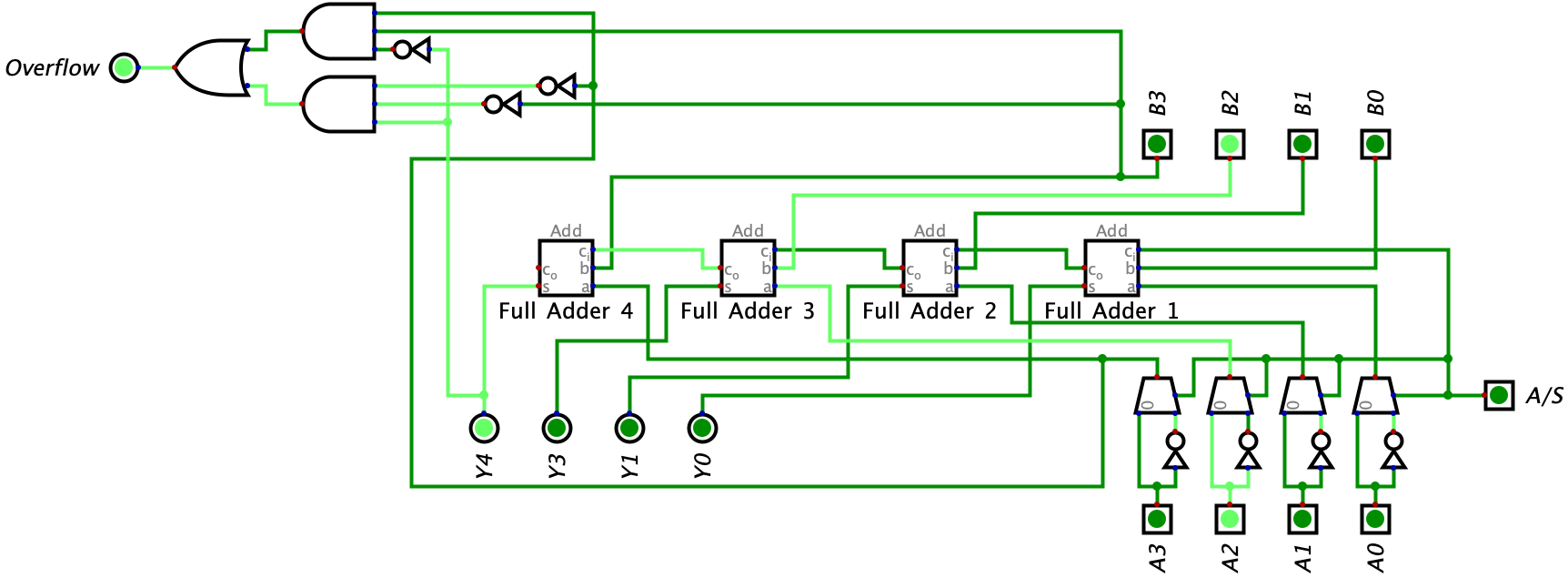
Next, let’s take a look at a subtraction example. Wen we do subtraction, the format or expression we use is \(B-A\) (since we are inverting the A input) and both B and A are in two’s complement form. In our example below, the value of B is \(0011_{2}\) and the value of A is \(0001_{2}\). So essentially, we are trying to solve for the expression \(3_{10}-1_{10}\).
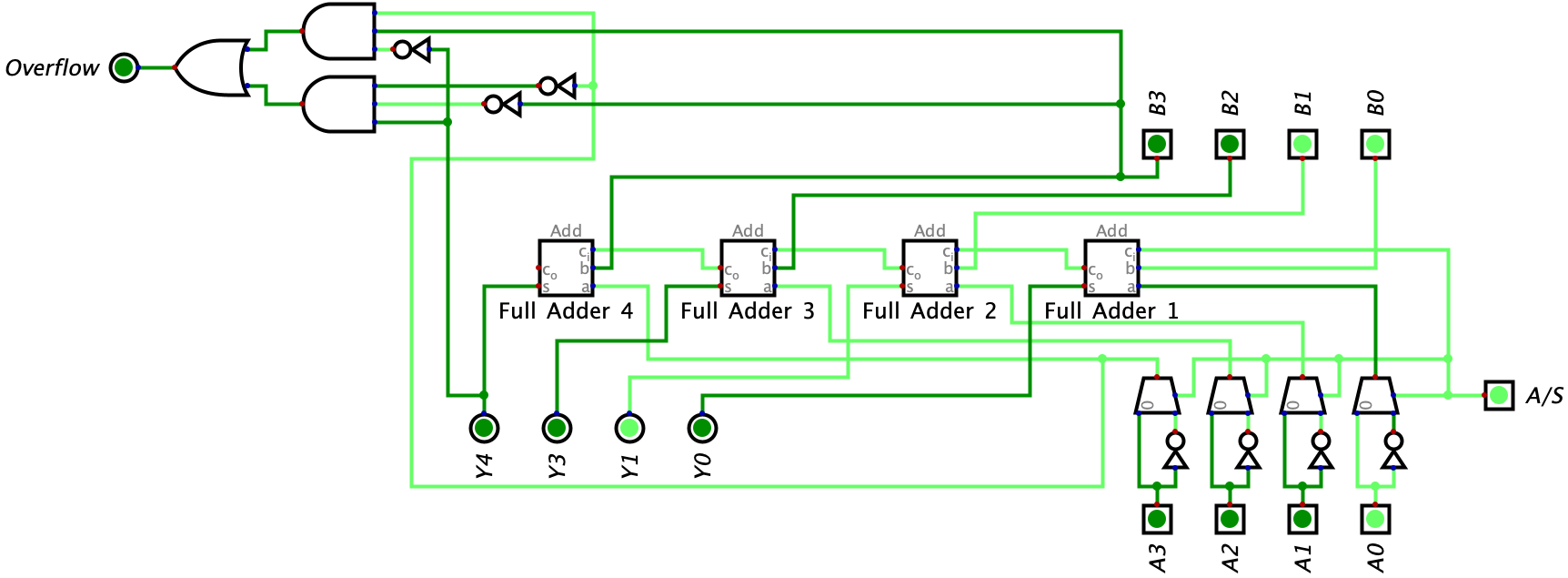
The last example we will take a look at is also a subtraction example, but it will result in overflow. In this example, the value of B is \(1000_{2}\) and the value of A is \(0010_{2}\). In other words, we are trying to represent the expression \(-8_{10}-2_{10}\) with our circuit.
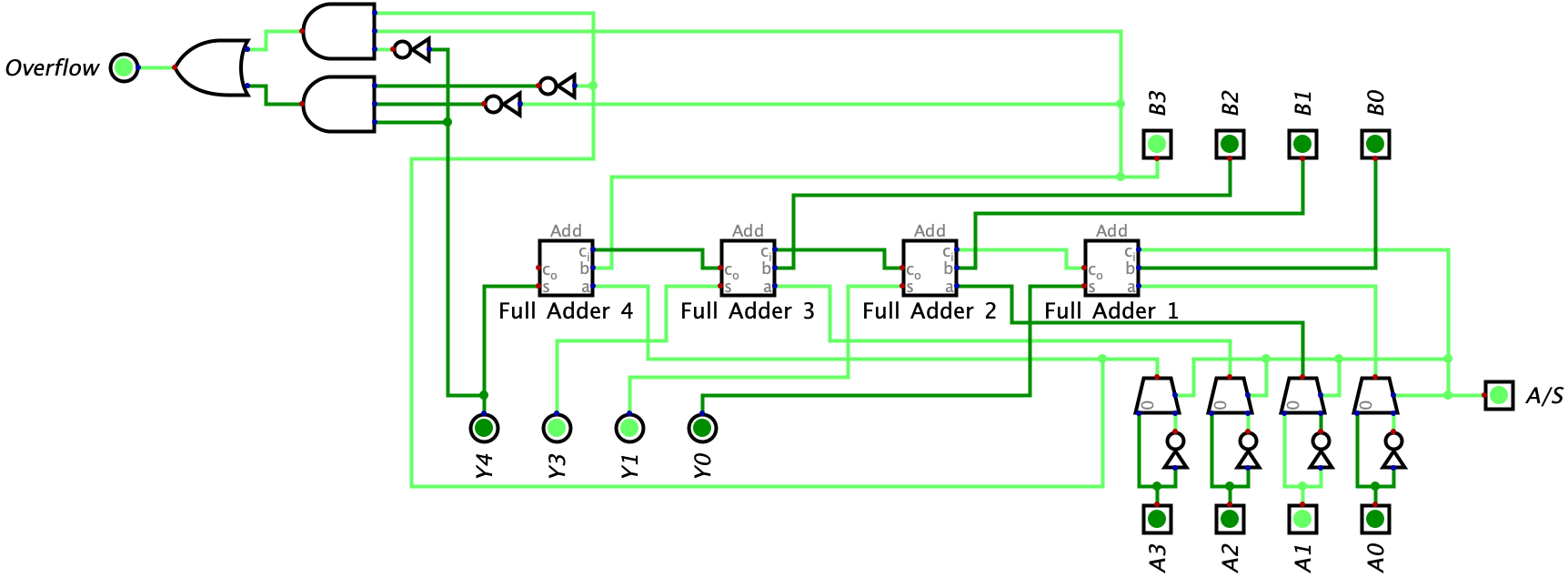
Wow, that was a lot of information. I would highly recommend understanding everything in detail in this chapter and playing around with the Digital files to really see how the circuits work. In the next chapter, we will be going over the ALU which uses the concept of an Adder-Subtractor and builds on it.